《高等数学》课程考试大纲
一、课程基本信息
1.课程性质:公共基础课
2.适用对象:怀化学院理、工、经、管类专业专升本招生考试
二、课程考试目的
《高等数学》课程考试旨在考察学生对微积分知识的掌握情况以及运用微积分知识解决实际问题的能力.
三、考试内容与要求
第一章 函数、极限与连续
(一)考试内容
一元函数的概念,函数的性质,反函数,基本初等函数的概念、性质及其图形,复合函数,初等函数,数列极限,函数极限,无穷小与无穷大,无穷小与极限之间的关系,无穷小与无穷大之间的关系,极限的运算法则,极限存在准则,两个重要极限,无穷小的比较,函数的连续性,函数的间断点及其分类,连续函数的运算定理,初等函数的连续性,闭区间上连续函数的基本性质.
(二)考试要求
1.理解函数、初等函数的概念;
2.了解函数的性质以及反函数的概念;
3.掌握基本初等函数的性质及其图形;
4.理解极限的概念,思想方法;
5.了解极限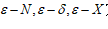 的定义;
的定义;
6.掌握左、右极限的概念,左、右极限与极限的关系;
7.掌握极限的四则运算法则;
8.了解两个极限存在准则,掌握两个重要极限;
9.理解无穷小的概念及与极限的关系;
10.了解无穷小的比较;
11.理解连续的两种定义,掌握连续性的证明方法、连续函数的运算性质,会判定间断点的类型;
12.理解闭区间上连续函数的性质,会用零点定理判别方程的根。
第二章 一元函数微分学
(一)考试内容
导数的概念,基本初等函数的导数,函数的和、差、积、商的导数,反函数和复合函数的导数,高阶导数,隐函数的导数,参数方程确定的函数的导数,微分的基本公式,微分形式不变性,微分在近似计算中的应用.
(二)考试要求
1.理解导数的概念,会利用概念求函数的导数;
2.掌握导数的几何意义,掌握求曲线的切线方程和法线方程的方法,了解可导与连续的关系;
3.掌握导数的运算;
4.理解微分的概念、几何意义、微分形式不变性,了解可导与可微的关系;
5.了解微分在近似计算中的应用;
第三章 一元函数微分学的应用
(一)考试内容
微分中值定理(罗尔定理、拉格朗日中值定理、柯西中值定理),罗必塔法则,泰勒公式,函数单调性的判别,函数的凸凹性及拐点的判别,函数的极值概念及求法,最大值与最小值的求法及其应用,函数图形的水平渐近线与铅直渐近线的求法.
(二)考试要求
1.了解三个微分中值定理的条件、结论,能证明前两个定理,了解构造函数的方法,掌握不等式的证明;
2.掌握洛必达法则的条件、结论以及常见的各种未定式极限的计算;
3.掌握泰勒公式和麦克劳林公式展开某些较简单的初等函数并求其近似值;
4.掌握函数的单调性、凹凸性、拐点、极值点的判别方法,会求曲线的水平渐近线和铅直渐近线;
5.掌握解决函数的最大值、最小值的求法,并能应用于求解实际问题。
第四章 一元函数积分学
(一)考试内容
定积分的概念,定积分的基本性质,微积分的基本定理,原函数与不定积分的概念,不定积分的基本性质,基本积分公式,换元积分法,分部积分法,有理函数的积分,三角函数有理式的积分,定积分的计算。
(二)考试要求
1.理解定积分的概念,几何意义,掌握定积分的性质;
2. 理解不定积分的概念、性质,了解不定积分的几何意义;
3.掌握不定积分的基本积分公式,掌握不定积分的基本求法;
4.掌握不定积分的两类换元积分和分部积分法;
5.掌握简单的有理函数、三角函数有理式、无理式的积分的求法;
6.掌握定积分的换元积分法和分部积分法;
7.理解变上限的定积分作为其上限的函数及其求导定理,熟悉牛顿-莱布尼兹公式和变上限积分函数的求导;
第五章 一元函数积分学的应用
(一)考试内容
积分元素法,定积分在求平面图形面积、几何体体积、曲线弧长、做功等物理量中的应用.
(二)考试要求
1.掌握定积分的积分元素法;
2. 掌握用定积分求平面图形面积、几何体体积、曲线弧长的方法;
3. 了解做功、水压力的计算方法;
第六章 微分方程
(一)考试内容
微分方程基本概念,可分离变量方程,齐次方程,一阶线性微分方程.
(二)考试要求
1.了解微分方程、阶、解、通解、初始条件和特解等概念;
2.会识别下列几种一阶微分方程:变量可分离的方程,一阶线性方程,齐次方程;
3.掌握变量可分离方程及一阶线性方程的解法;
4.了解微分方程解决简单的几何问题和物理问题的方法。
第七章 向量与空间解析几何
(一)考试内容
空间直角坐标系,两点间距离公式,向量代数,直线、平面的方程,常见曲面及其方程.
(二)考试要求
1.了解空间直角坐标系,能建立空间点与数组的一一对应关系;
2.掌握两点间距离公式,了解向量的运算(线性运算、点乘法、叉乘法),掌握两个向量夹角的求法与垂直、平行的条件;
3.掌握利用坐标表达式进行向量运算的方法;
4.掌握平面、直线的方程及求法;
5.了解常见曲面的几何形状及方程。
第八章 多元函数微分学
(一)考试内容
二元函数的概念,二元函数的图像,二元函数的极限、连续,偏导数的概念,高阶偏导数、全增量与全微分,全微分存在的条件,多元复合函数微分法,隐函数及其微分法.
(二)考试要求
1.理解二元函数的概念,了解二元函数的几何意义;
2.了解二元函数的极限、连续性等概念以及有界闭域上连续二元函数的性质;
3.理解偏导数、全微分等概念并掌握其计算方法,了解全微分存在条件;
4.掌握复合函数的偏导数的求法;
5.掌握求隐函数所确定的函数的偏导数的方法;
第九章 多元函数微分学的应用
(一)考试内容
空间曲线的切线和法平面,空间曲面的切平面与法线,方向导数,二元函数的极值,最大值、最小值及其应用.
(二)考试要求
1.掌握空间曲线的切线和法平面、空间曲面的切平面与法线的求法;
2. 理解方向导数的概念;
3.理解多元函数极值的概念,会求函数的极值;
4. 了解条件极值的概念,会用拉格朗日乘数法求条件极值;
5.会求一些较简单的多元函数的最大值和最小值的应用问题。
第十章 多元函数积分学(I)
(一)考试内容
二重积分的概念及性质,二重积分的计算,二重积分的应用,对弧长的曲线积分,对面积的曲面积分。
(二)考试要求
1.理解二重积分的概念,了解二重积分的性质;
2.掌握直角坐标下二重积分的计算方法;
3.了解极坐标下二重积分的计算方法;
4.会应用二重积分求面积、体积、薄片质量;
5. 理解对弧长的曲线积分的定义和性质;
6. 掌握对弧长的曲线积分的计算方法;
7. 了解对面积的曲面积分的定义、性质和计算方法。
第十一章 多元函数积分学(II)
(一)考试内容
对坐标的曲线积分,对坐标的曲面积分;
(二)考试要求
1. 理解对坐标的曲线积分的定义和性质;
2. 掌握对坐标的曲线积分的计算方法;
3. 了解对坐标的曲面积分的定义、性质和计算方法。
四、考试方式及时间
1.考试方式:闭卷
2.考试时间:120分钟
五、考试题型结构及分值分布
1. 考试题型结构:单项选择题,填空题,判断题,计算题,证明题。
2. 分值分布(满分 100分):
(1)单项选择题(每小题3分,共15分);
(2)填空题(每小题4分,共20分);
(3)判断题(每小题2分,共10分);
(4)计算题(每小题7分,共42分);
(5)证明题、综合题(共13分),
六、教材与参考书目
1.高等数学(上),黄立宏 主编,北京大学出版社, ISBN:9787301295045
2. 高等数学(下),黄立宏 主编,北京大学出版社, ISBN:9787301295076
3. 高等数学(第七版)(上册),同济大学应用数学系 编,高等教育出版社,ISBN:9787040396638.
4. 高等数学(第七版)(下册),同济大学应用数学系 编,高等教育出版社,ISBN:9787040396621 .
怀化学院公共数学教研室
附 录(题型举例)



《无机化学》专升本考试大纲
一、 课程信息
课程性质:专业基础课(必修)
适用专业:材料化学
考试对象:材料化学专业专升本学生
课程学时:56学时/3.5学分
二、课程考试目的及考核目标
以材料化学专业本科生人才培养方案中对本科生的基础知识能力要求为目标,无机化学课程 考试旨在考察学生对无机化学中的基本原理、基本理论及基础知识的掌握程度,为后续专业课程的学习打下坚实基础,为从事专业相关工作提供知识及能力支撑。
三、考试范围
第一章 化学基础知识
(一)考试内容
1、混合气体分压定律
2、稀溶液依数性及应用
3、溶液浓度表示方法
(二)考试要求
掌握理想气体状态方程及混合气体分压定律、掌握稀溶液的依数性及应用,掌握溶液浓度表示方法,熟悉溶液饱和蒸气压,明确学习本课程对于未来其它化学课程及专业课程学习的重要作用,激发学生学习的兴趣与热情,为以后各章学习打下基础。
第二章:化学热力学基础
(一)考试内容
1、状态函数性质
2、盖斯定律
3、焓、熵、吉布斯自由能的含义及化学反应过程中的反应焓、反应熵、吉布斯自由能的求解
4、利用吉布斯自由能判断反应进行方向及逆转温度
(二)考试要求
掌握状态函数的基本概念,掌握化学反应进度的概念及反应进度求解,掌握盖斯定律,掌握标准生成热的定义,掌握焓、熵、吉布斯自由能的含义及化学反应过程中的反应焓、反应熵、吉布斯自由能的求解,利用吉布斯自由能判断反应进行方向及逆转温度,熟悉热力学第一、第二、第三定律,熟悉化学反应的热效应,理解燃烧热,理解可逆途径。
第三章:化学反应速率
(一)考试内容
1、反应速率的概念、速率方程、反应级数及速率常数
2、反应机理
3、反应物浓度与时间的关系
4、温度对反应速率的影响
5、催化剂与催化反应
(二)考试要求
反应速率的概念、速率方程的表示、反应级数及速率常数求解,掌握反应物浓度与时间的关系求解,掌握温度对反应速率的影响,熟悉催化剂对反应的影响,了解反应机理及反应速率理论。
第四章:化学平衡
(一)考试内容
1、化学反应等温式
2、平衡常数的相关计算
3、用平衡常数判断化学反应方向
4、化学平衡的移动
(二)考试要求
掌握标准平衡常数的定义,掌握用平衡常数判断化学反应方向的方法,掌握化学反应等温式子(特霍夫等温方程式),掌握化学平衡的移动及相关计算,熟悉平衡转化率,了解经验平衡常数。
第五章:原子结构和元素周期律
(一)考试内容
1、核外电子运动状态的描述(四个量子数)
2、多电子原子的能级、原子核外电子排布规律
3、元素基本性质(原子半径、电离能、电子亲和能及电负性)的周期性
(二)考试要求
掌握四个量子数及原子和外电子排布规律,掌握元素周期表的分区,掌握原子半径、电负性随周期变化的规律,熟悉核外电子运动状态的图形描述,了解近代原子结构的确立及微观粒子运动的特殊性。
第六章:分子结构和共价键理论
(一)考试内容
1、共价键理论及共价键的基本性质
2、杂化轨道理论与分子空间构型
3、价层电子互斥论与分子空间构型
(二)考试要求
掌握价键理论基本知识及共价键基本性质,掌握杂化轨道理论基本知识,熟悉价层电子互斥论。
第七章 晶体结构
(一)考试内容
1、分子间作用力
2、离子晶体和离子键
3、次级键及氢键
(二)考试要求
掌握分子间作用力的分类和特点,熟悉离子键的性质,熟悉氢键及次级键,了解离子的特征和离子晶体,了解离子极化及离子极化对化合物性质的影响。
第八章 酸碱解离平衡
(一)考试内容
1、一元弱酸弱碱的解离平衡
2、多元弱酸弱碱的解离平衡
3、缓冲溶液构成、性质及配置计算
4、盐的水解
(二)考试要求
掌握一元弱酸、弱碱的解离平衡及计算,掌握多元弱酸、弱碱的解离平衡及计算,熟悉缓冲溶液的配制计算,熟悉盐的水解与水解平衡计算,了解强电解质溶液理论,了解酸碱电子论及酸碱溶剂论。
第九章 沉淀溶解平衡
(一)考试内容
1、溶度积常数及计算
2、溶度积与溶解度的关系及换算
3、溶度积原理
4、沉淀的生成计算及应用
(二)考试要求
掌握溶度积常数基本概念及求解计算,掌握溶度积原理,掌握溶度积和溶解度的关系及相互换算,熟悉沉淀的生成计算及应用,了解沉淀的溶解与转换。
第十章 氧化还原反应
(一)考试内容
1、电极电势及电动势
2、电池反应热力学
3、电动势和标准电动势的关系(能斯特方程)
4、影响电极电势的因素
(二)考试要求
理解化合价和氧化数,掌握原电池表示方法及电池符号书写,掌握电极电势和电动势,掌握电池反应热力学及能斯特方程的应用,熟悉影响电极电势的因素,了解化学电源和电解,了解图解法讨论电极电势。
第十一章 配位化学基础
(一)考试内容
1、配合物命名
2、配合物的构型、中心价层轨道的杂化
3、配合物的稳定性
(二)考试要求
掌握配位化合物的命名,掌握配合物的价键理论,熟悉配合物的稳定性,了解配位化合物的晶体场理论。
四、考试方式及时间
1、考试方式:闭卷
2、考试时间:120分钟
五、考试题型及分值分布
1、单项选择题 30分
2、填空题 20分
3、判断题 10分
4、简答题 16分
5、计算题 24分
说明:每题型的分值可根据实际情况稍有调整。
六、教材与参考书目
1、教材
《无机化学》上册,第四版,宋天佑、程鹏等人编写,高等教育出版社,2019.
2、参考书目
(1)《无机化学》,第六版,孟长功主编,高等教育出版社,2018.
(2)《无机及分析化学》,第五版,南京大学编写组,高等教育出版社,2015.
附录:题型举例



《材料工程基础》课程考试大纲
一、课程基本信息
1、课程编号:
2、课程性质:专业必修课
3、适用专业:材料化学本科
4、考试对象:材料化学专升本考生
5、学时/学分:80学时,3学分
二、课程考试目的
材料工程基础课程的考试旨在考察学生材料工程领域中的共性基础理论——动量、能量和质量传递的基本规律,以及上述理论典型运用的单元过程——物料的干燥和燃烧过程的基本理论和基本知识,强调理论知识与工程实践相结合,为从事材料工程领域中科研、设计、生产工作打下良好基础。
三、考试内容及要求
第一章 流体力学基础
(一)考试内容
流体的概念及其特点、性质,流体力学的研究内容,描述流体运动的两种方法,作用在流体上的力——质量力和表面力,牛顿粘性定律、傅里叶定律、斐克定律的表达式及各符号所表达的意义,理想流体的伯努利方程式及其应用,实际流体的伯努利方程式及其应用。
(二)考试要求
1、掌握流体特点和性质,牛顿粘性定律、傅里叶定律、斐克定律的表达式及各符号所表达的意义,理想流体的伯努利方程式及其实际应用,实际流体的伯努利方程式及其实际应用。
2、熟悉作用在流体上的力——质量力和表面力的概念及其举例。
3、了解流体力学的研究内容,描述流体运动的两种方法。
第二章 两相运动
(一)考试内容
相、两相流的基本概念,喷雾干燥、离心分离、气力输送、流化床的概念及特点,单粒子在流体中的受力分析,包括阻力、非稳定力和不均匀流场对粒子的作用力。
(二)考试要求
1、掌握单粒子在流体中的受力分析,包括阻力、非稳定力和不均匀流场对粒子的作用力;非稳定力中虚拟质量力和Basset力的概念;不均匀流场对粒子的压强梯度力和升力的概念。
2、熟悉相、两相流的基本概念。
3、了解喷雾干燥、离心分离、气力输送、流化床的概念及特点。
第三章 传热学基础
(一)考试内容
热量传递的基本方式及其概念,区别热对流和对流换热、热辐射和辐射换热的概念,温度场和温度梯度,导热系数,单层平壁导热计算。
(二)考试要求
1、掌握热量传递的基本方式及其概念,单层平壁导热计算。
2、熟悉热对流和对流换热、热辐射和辐射换热的概念及区别,导热系数的意义。
3、了解温度场和温度梯度的概念及意义。
第四章 质量传递基础
(一)考试内容
传质的基本概念,斐克定律的表达式及物理意义,流体中等摩尔逆向扩散及单向扩散,多孔固体中的稳态扩散。
(二)考试要求
1、掌握传质的基本概念,斐克定律的表达式及物理意义;
2、熟悉流体中等摩尔逆向扩散及单向扩散;
3、了解多孔固体中的稳态扩散。
第五章 物料干燥
(一)考试内容
固体物料的去湿方法,物料的干燥方法及其特点,湿空气的性质,水分在气-固两相间的平衡,干燥曲线和干燥速率曲线,干燥技术。
(二)考试要求
1、掌握水分在气-固两相间的平衡,结合水与非结合水、平衡水分和自由水分的概念及区别,干燥曲线和干燥速率曲线每个阶段所表示的意义及特点;
2、熟悉固体物料的去湿方法分类及特点,物料的干燥方法及其特点,湿空气的性质,湿空气中水蒸气的量的表示方法及湿空气的各类参数;
3、了解典型的干燥技术。
第六章 燃料及其燃烧
(一)考试内容
燃烧的概念,燃料的种类,燃料的组成及表示方法,煤、燃料油、气体燃料的特性。
(二)考试要求
1、掌握燃烧的概念,固体燃料和燃料油的组成及其两种表示方法;
2、熟悉燃料的种类,煤、燃料油、气体燃料的特性。
四、考试方式及时间
1、考试方式:闭卷
2、考试时间:120分钟
五、考试题型结构及分值分布
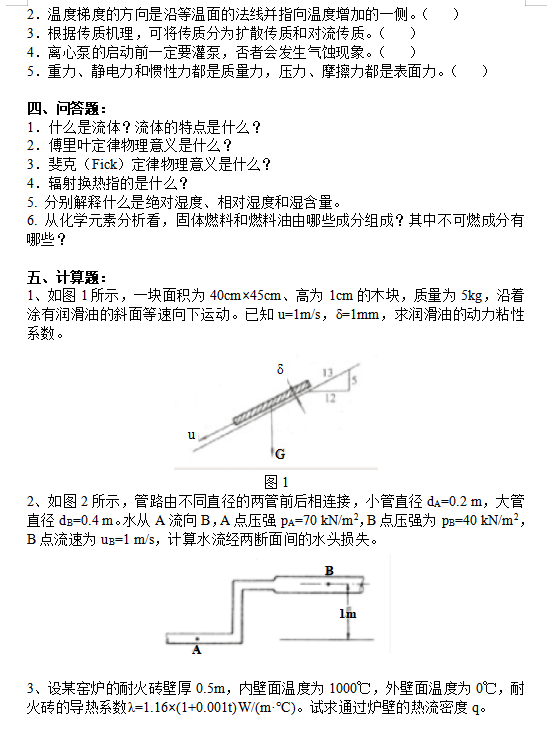
试卷题型比例:选择题20分,填空题20分,是非题20分,问答题20分,计算题20分。
六、教材与参考书目
1、教材:徐德龙、谢峻林主编《材料工程基础》,第一版,武汉:武汉理工大学出版社2008
2、参考书目:
冯晓云主编《材料工程基础》,第一版,北京:化学工业出版社2007
附录:题型举例

原网址:http://zsb.hhtc.edu.cn/info/1022/1945.htm